如果你了解过 Uniswap V2,你一定知道它最大的优点是“完全自动化”,最大的问题也是“完全自动化”。资金一旦进入,都会机械地分布在从0到∞的整个价格区间。
这本来很公平,却非常低效:
大多数时间,资产都在远离市场价格的位置“睡觉”,没有人交易到那里,也不产生手续费。
于是,Uniswap V3 提出一个革命性的概念:集中流动性(Concentrated Liquidity)。
它让 LP 可以把资金“集中”在自己认为合适的价格范围内,让“活钱干活”。
一、什么是集中流动性:背景与要解决的问题
去中心化交易合约 Uniswap 采用自动做市商(AMM)模型,用户无需挂单,也无需寻找对手方,只要向池子中注入两种代币,就可以成为流动性提供者。这种模式非常简洁,但也带来了一个不易察觉的问题:大部分流动性并没有发挥作用。
为了说明这一点,我们需要先回顾 Uniswap v2 的机制。
1. 传统 AMM:恒定乘积与“全价格区间”
在 v2 的恒定乘积模型中,交易池中维持一个恒定公式:
x · y = k
这里的 x 和 y,是池中两种资产的数量,k 是常数。无论市场价格如何波动,这个公式总是成立。
但这个模型隐含一个设定:池子的流动性分布在从 0 到 ∞ 的整个价格范围上。理论上无论价格涨到多高、跌到多低,这个池子都“准备好”提供流动性。
问题是:真实市场的价格从来不会走到 0 或无穷大。
换句话说,流动性被被动地散布在一个几乎永远用不上的超级宽区间里。
2. 流动性利用率的问题
如果流动性分布在一个过大的范围上,会造成一个非常直接的后果:
绝大部分资金是在“睡觉”。
现实中,价格通常在一个较窄范围内波动,因此真正参与交易的,只是这个范围以内的资金。而其他资金只是静静地躺着,却仍然需要占用资本。
于是就出现两个影响:
- 对交易者来说,主动成交的深度有限,滑点高;
- 对 LP 来说,明明投入很多资金,收益却并不成比例。
换句话说:
资金利用率低。
3. 为什么需要集中流动性
Uniswap 在 v3 版本提出集中流动性(Concentrated Liquidity),核心思想非常直接:
流动性应当放在实际会发生交易的价格区间里。
如果价格长期在一个区域波动,那 LP 就可以把流动性集中在这个区域,不再浪费在可能根本不会出现的极端价格上。
这样带来的效果是显著的:
- 同样的资金,提供更深的流动性
- 对大额交易的价格冲击减小
- 手续费收入提高
这实际上把 AMM 从“广泛分布”改成了“局部有效分布”。
4. 集中流动性的定义
严格来说,集中流动性是指:
LP 只在自己设定的价格区间 \([P_{lower}, P_{upper}]\) 内提供流动性,一旦价格超出范围,就不再参与交易,也不再赚费。
这意味着,每一个 LP 不再是一个简单的资金池,而变成一个“带有条件的流动性头寸”。
从合约的角度看,是把一个大池子拆成很多小区间,把流动性分别放入这些区间,交易发生在哪个区间,哪个区间的 LP 就得到手续费。
5. 它解决的到底是什么问题
如果用一句话概括:
用同样的资本,获得更高的有效深度。
但具体来说,它带来三项核心改进:
- 提高资本效率
- 降低滑点
- 提高 LP 的费收益率
这些优点都来自同一个事实:流动性终于可以集中,而不是无边界地稀释。
6. 但它并不是免费的优化
集中流动性并没有改变 AMM 的基本逻辑,而是引入一个新的维度:价格区间。
这让 LP 的岗位变得更像需要判断价格趋势的“策略性角色”。因此,集中流动性同时带来了一个新的风险:
- 如果价格突破区间,头寸会变成单边资产,并停止产生收益。
为了获得更高的收益,需要承担更多管理与判断成本。这是一种典型的“收益与风险互换”关系。
二、集中流动性是如何运行的
1. 提供流动性需要输入什么
假设我们向 ETH/USDC 池子提供流动性,合约会要求我们输入:
-
币对:ETH / USDC
-
价格区间
- lower price 例:2000 USDC/ETH
- upper price 例:3000 USDC/ETH
-
想提供多少 ETH 或多少 USDC
也就是说,我们其实是在告诉合约三件事:
- 我想参与 ETH / USDC 交易对的做市
- 在 2000~3000 这个区间
- 我愿意提供多少币
2. 需要提供什么代币
假设当前 ETH/USDC 价格是 2500,那么系统判断为:
2000 < 2500 < 3000
也就是“价格在区间内”。
这个判断非常重要,因为它直接影响我们需要提供的资产结构:
三种情况
| 当前价格 | 需要提供 |
|---|---|
| 在区间内 | 需要同时提供 ETH 和 USDC |
| 当前价格低于区间 | 只会用到 USDC |
| 当前价格高于区间 | 只会用到 ETH |
为什么会这样?它不是策略,而是数学决定的:AMM 会在不同价格状态下,自动将持仓偏向一种资产,这由模型决定,不是策略行为。
简单地理解就是,物以稀为贵。当价格较低时,交易池需要更多的 USDC,当价格较高时,交易池需要更多的 ETH。
3. 理解流动性
虽然我们给的是资产(ETH/USDC),但合约内部记录的是一个抽象量 L(流动性单位)。
理解要点:
- 我们投入的是资产
- 合约记录的是 L
- 我们未来赚的钱与 L 成正比
更直观说:
L 就像我们在这个价格区间的“份额大小”。
而 ETH / USDC 的数量,会随着价格变化自动调整。
4. 价格区间离散化
我们给的区间是连续价格(比如 2000→3000),但合约内部用 tick 记录价格。
合约会把它们转成:
- \(tick_{Lower}\)
- \(tick_{Upper}\)
tick 是一个离散价格,用来标记区间边界。
这一步之后,合约会为这个区间范围增加相应的流动性,实际记录方式为只记录边界状态:
- 在 \(tick_{Lower}\) 位置把流动性 +L
- 在 \(tick_{Upper}\) 位置把流动性 -L
这样,当前活跃的流动性等于所有当前价格以下的净流动性之和:
\[ activeLiquidity = \sum (netLiquidity < \text{current tick}) \]比如 \(tick_{Lower}=100\), \(tick_{Upper}=200\),合约会记录为
netLiquidity[100] += 10
netLiquidity[200] -= 10
如果当前价格 tick 是 150,那么 activeLiquidity 等于所有 tick < 150 的 netLiquidity 之和,也就是10
如果当前价格 tick 是 205,那么 activeLiquidity 等于所有 tick < 205 的 netLiquidity 之和,也就是0
所以,当价格穿过这些 tick 时,系统就知道应该在什么时候开始、什么时候结束使用我们的流动性。
为什么在存储区间时,要对价格进行离散处理?
如果用线性划分,当 ETH/USDC 的价格在 2000~3000 区间时,简单切 1000 段,每段 1USDC,当然可以,看起来也很自然。
但是如果价格区间变为 0.2~0.3 或者更低呢?还是按照切 1000 段,就会导致每段区间过小,整体刻度是极不均匀的。
而且真实情况下,不同代币的价格可能跨越几个数量级,从 0.0000001 到 10000000 都可能,因此也无法为所有的币统一刻度。
如何进行离散处理呢?
我们设定每个刻度对应的价格是前一个刻度对应价格的固定倍数 \(r\),那么对于tick+1刻度的价格 \(P_{tick+1}\) 有以下公式
\[ P_{tick+1} = P_{tick} \times r \]
由此就很容易推导出以下公式
\[ P_{tick} = P_0 \times r^{tick} \]
如果设定初始值 \(P_0=1\),常量 \(r=1.0001\),则可以得到
\[ P_{tick} = 1.0001^{tick} \]
这意味着每次 tick 移动,价格变 0.01%。
现在我们就可以将任意价格使用tick表示
\[ tick = log_{1.0001}P \]
比如
\(P=0.25\) 对应的 \(tick\approx-13864\)
\(P=2500\) 对应的 \(tick\approx78244\)
那么我们的均匀刻度就设计好了,它可以适用于任意价格的代币(只要价格不是负数🤪)
5. 保存流动性状态
当我们添加流动性时,系统会给我们分配一个 NFT,它记录:
- 选择的区间(2000~3000)
- L 的大小
- 已经累计能够领取的手续费
- 后续计算手续费需要用到的当前 fee 状态
因此:
做市行为不再是池子的一部分,而是一个 NFT 记录的独立头寸。
6. 持仓变化
当价格在区间内:
- 同时持有 ETH 和 USDC
- 随着交易发生,两者互相转换
- 参与撮合并赚手续费
如果价格跌破 2000:
- 头寸会变成全部 USDC
- 不再参与做市,也停止赚手续费
如果价格突破 3000:
- 头寸会变成全部 ETH
- 同样退出做市
换句话说:
ETH 涨,头寸更偏 ETH;ETH 跌,头寸更偏 USDC。
这个行为不是策略,而是 AMM 自动完成的结果。
7. 手续费结算
交易发生在区间内(2500在内),就会累积手续费。合约内部会把手续费累计到该区间的 feeGrowth 中。
提现时合约会做两件事:
- 返回当前持仓(可能是 ETH+USDC,可能是单币)
- 返回累计所得手续费
不需要手动领,提现时自动结算。
三、主要公式推导
1. 官方白皮书
v2链接: https://docs.uniswap.org/whitepaper.pdf
v3链接: https://app.uniswap.org/whitepaper-v3.pdf
v4链接: https://app.uniswap.org/whitepaper-v4.pdf
2. 基础公式
虚拟资金池曲线(交易模型)
\[ x \times y = k \tag{1} \]流动性
\[ L = \sqrt{xy} \tag{2} \]价格
\[ P = \frac{y}{x} \tag{3} \]有效资金池曲线
\[ (x+\dfrac{L}{\sqrt{p_{b}}})(y+L\sqrt{p_{a}})=L^{2} \tag{4} \]2. 有效资金池曲线推导
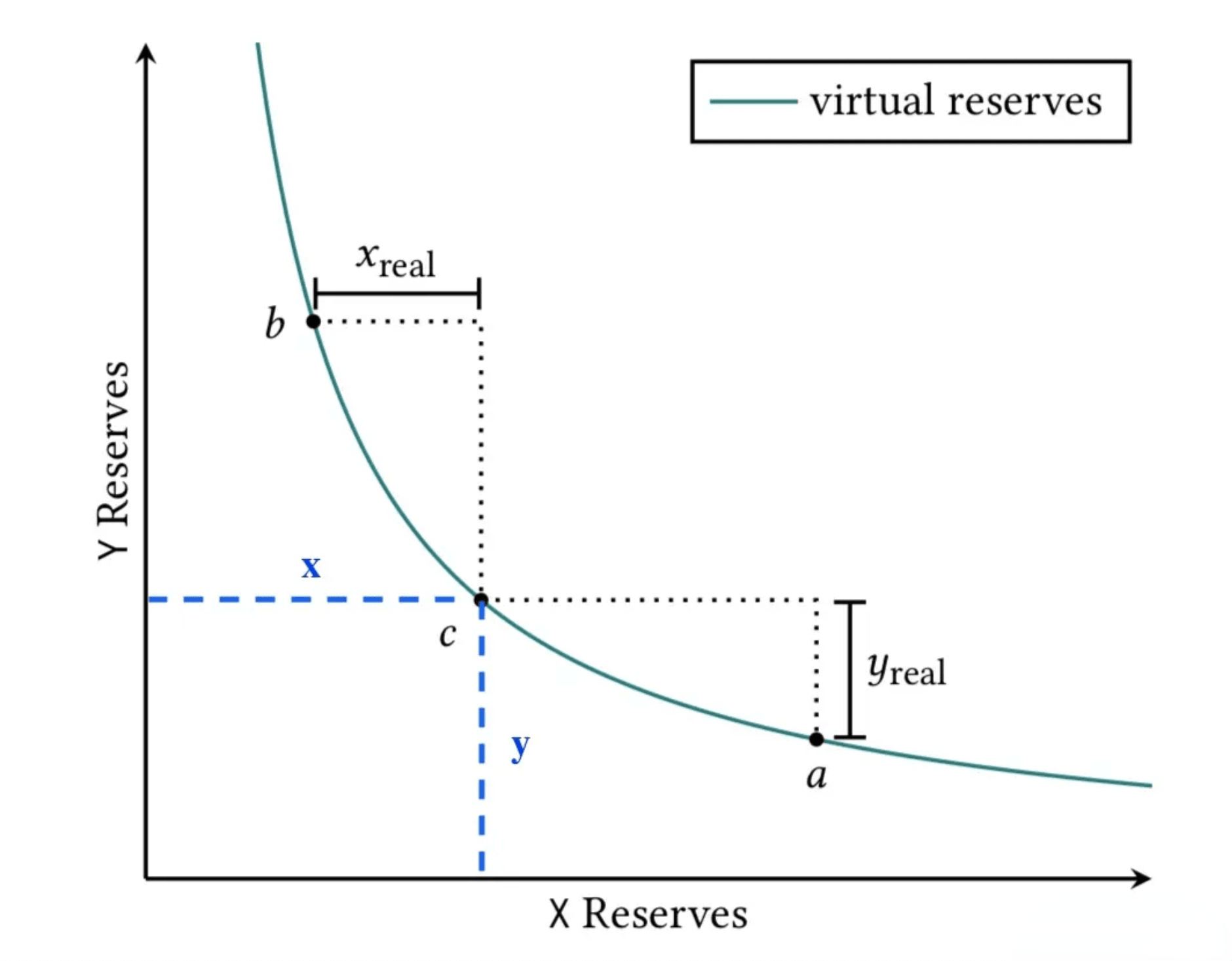
根据上图1所示,当前价格在 c 点,假设实际价格的波动范围为 [a,b]
那么当价格从 c 点向 a 点滑动时,资金池的消耗最大为 \(y_{real}\) ,同理,当价格由 c 点向 b 点滑动时,资金池的消耗最大为 \(x_{real}\)
因此,理论上只需要提供 \(x_{real}\) 和 \(y_{real}\) 就够了,其余的资金是永远都用不上的,这也说明了为什么xyk基础模型的资金利用率低
那么问题来了,实际有效的资金池曲线应该是什么样的呢?
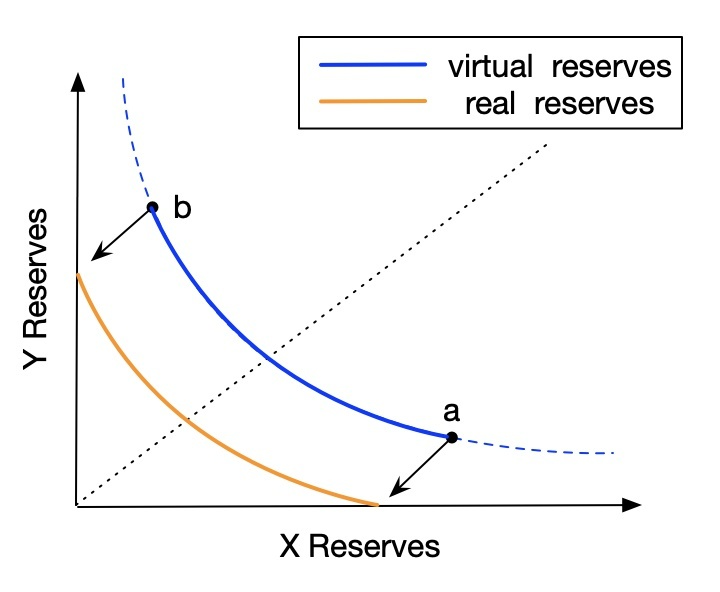
如上图2所示,我们开始推导这个有效资金池曲线公式
\[ L^2 = xy \\ P = \frac{y}{x} \]对于攻读过初中数学学位的人来说,将等式两边相乘和相除就可以轻松推导出以下公式
\[ \begin{aligned} x=\dfrac{L}{\sqrt{P}} \\ y=L\sqrt{P} \tag{4} \end{aligned} \]由图1可知
\[ x=x_{real}+x_b \\ y=y_{real}+y_a \]代入公式 (1) 的 xyk 模型可得
\[ (x_{real}+x_b)(y_{real}+y_a)=k=L^2 \]再根据公式 (4) 将 \(x_b, y_a\) 替换可得
\[ (x_{real}+\dfrac{L}{\sqrt{P_{b}}})(y_{real}+L\sqrt{P_{a}})=L^{2} \]这就是最终的有效资金池曲线了
3. 计算流动性变化
我们提供流动性后,合约开始进行各种交易行为,那么要如何计算当前我们提供的流动性中资产是如何分配的?
根据上面的公式(4):
\[ \begin{aligned} x=\dfrac{L}{\sqrt{p}} \\ y=L\sqrt{P} \tag{4} \end{aligned} \]令:
\[ \begin{aligned} S = \sqrt{P} \end{aligned} \]则:
\[ \begin{aligned} x=\dfrac{L}{S} \\ y=LS \end{aligned} \]因为 L 不变,对 S 求微分:
对 x:
\[ x = \frac{L}{S} \Rightarrow dx = -L \frac{1}{S^2} dS \]对 y:
\[ y = L S \Rightarrow dy = L dS \]所以有两条很重要的微分关系:
\[ dx = -L \frac{1}{S^2} dS,\qquad dy = L dS \]假设一个 LP 的有效价格区间是:
- 下界价格:\(P_a\),对应 \(S_a = \sqrt{P_a}\)
- 上界价格:\(P_b\),对应 \(S_b = \sqrt{P_b}\)
只看 \(token_y\) 的变化
在区间内,S 从 (S_a) 增长到 (S_b) 时:
\[ dy = L dS \]对 S 从 (S_a) 到 (S_b) 积分:
\[ \Delta y = \int_{S_a}^{S_b} L, dS = L (S_b - S_a) = L(\sqrt{P_b} - \sqrt{P_a}) \]这就是 在整个 \([P_a, P_b]\) 区间里对应的 \(token_y\) 数量:
\[ amount_y = L(\sqrt{P_b} - \sqrt{P_a}) \]只看 \(token_x\)的变化
对 \(token_x\):
\[ dx = -L \frac{1}{S^2} dS \]注意: x 和 S 方向相反(价格上升 → \(token_x\) 减少), 我们要的是区间内总共的 \(token_x\) 数量,取绝对值来算:
\[ \Delta x = \int_{S_a}^{S_b} L \frac{1}{S^2} dS \]计算:
\[ \int \frac{1}{S^2} dS = -\frac{1}{S} \]所以:
\[ \Delta x = L\left[-\frac{1}{S}\right]_{S_a}^{S_b} = L\left(-\frac{1}{S_b} + \frac{1}{S_a}\right) = L\left(\frac{1}{S_a} - \frac{1}{S_b}\right) \]代回 \(S = \sqrt{P}\):
\[ amount_x = L\left(\frac{1}{\sqrt{P_a}} - \frac{1}{\sqrt{P_b}}\right) \]这就是 \(token_x\) 的区间公式。
上面推导的是整个 \([P_a, P_b]\) 区间的总 x/y。 但实际情况取决于当前价格 (P) 在区间里的位置:
情况 A:当前价格在区间内部(\(P_a < P < P_b\))
这时的头寸是“部分在 token0,部分在 token1”:
-
对 \(token_x\),有效区间是 [P, Pb] (高价端还没被换走的 \(token_x\))
\[ amount_x = L\left(\frac{1}{\sqrt{P}} - \frac{1}{\sqrt{P_b}}\right) \] -
对 \(token_y\),有效区间是 [Pa, P] (从下界到现在已经变成 \(token_y\) 的部分)
[ amount_y = L(\sqrt{P} - \sqrt{P_a}) ]
情况 B:价格低于区间(\(P \le P_a\))
还没开始“向上走”,流动性全部在 \(token_x\) 形态:
\[ amount_x = L\left(\frac{1}{\sqrt{P_a}} - \frac{1}{\sqrt{P_b}}\right) \\ \quad amount_y = 0 \]情况 C:价格高于区间(\(P \ge P_b\))
已经“完全向上走完”,全部变成 \(token_y\):
\[ amount_x = 0 \\ \quad amount_y = L(\sqrt{P_b} - \sqrt{P_a}) \]4. 计算实际交易价格
我们已经知道了交易原理和基本公式,那么当我们准备通过交易池兑换代币时,因为我们投入的资产也会影响交易池的资产比例,\(P=\dfrac{y}{x}\) 只是理论价格,那么应该如何计算实际交易价格呢?比如说1个 ETH 能换多少 USDC ?
当我们往池子里投入 \(\Delta x\) 个 ETH 时,池中的 USDC 会减少 \(\Delta y\),对应的价格也会从 \(P_0\) 下跌到 \(P_1\),于是有以下关系
\[ \begin{aligned} \Delta x &= L\left(\frac{1}{\sqrt{P_1}} - \frac{1}{\sqrt{P_0}}\right) = L\left(\frac{1}{S_1} - \frac{1}{S_0}\right) \Rightarrow S_1 = \frac{1}{\dfrac{\Delta x}{L} + \dfrac{1}{S_0}} \\ \Delta y &= L(\sqrt{P_0} - \sqrt{P_1}) = L(S_0 - S_1) = L\left(S_0 - \frac{1}{\dfrac{\Delta x}{L} + \dfrac{1}{S_0}}\right) \end{aligned} \]其中,L为当前区间的流动性。
如果交易量很大、会跨 tick,就把区间拆成多段,对每一段用同样的方法算一段,然后把每一段的 Δy 累加起来即可。